The laser pulse (150 fsec, 780nm) has been focused by a lens of 5 cm focal length into a supersonic Argon gas jet. The ions were guided by a weak electric field (3.5 V/cm) onto a position sensitive channel plate detector with delay-line readout. From the position of impact and the time-of-flight the three dimensional momentum vector can be determined. The electrons are guided by the electric field and a parallel magnetic field (10.4 Gauss) onto a second position sensitive detector. The electron momentum vector is determined from the time-of-flight and the position of impact.
click on the image above to see an animation of the process (175kb).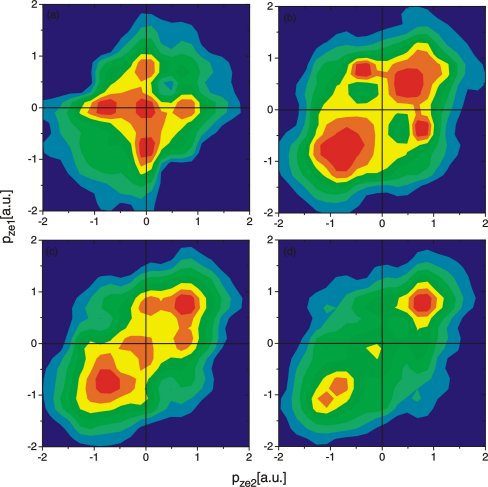

One of the electrons has a transverse momentum of:
(a) 0.0<p_perp<0.1 a.u. (b) 0.1<p_perp<0.2 a.u. (c) 0.2<p_perp<0.3 a.u. (d) 0.3<p_perp<0.4 a.u.
The color coding shows the differential rate in arbitrary units. The vertical axis shows the momentum component of the one electron in the direction of polarization (p_ez1) and the horizontal axis the same momentum component of the other electron. For one of the electrons the transverse momentum has been fixed to a certain interval.

We observe a strong dependence of the correlation pattern on this transverse momentum. If one electron is emitted off the polarization axis, then both electrons are found to have most likely similar parallel momenta (figure d). In contrast if one electron is fixed along the polarization with very small transverse moment (figure a), then we find mostly one fast and one slow electron.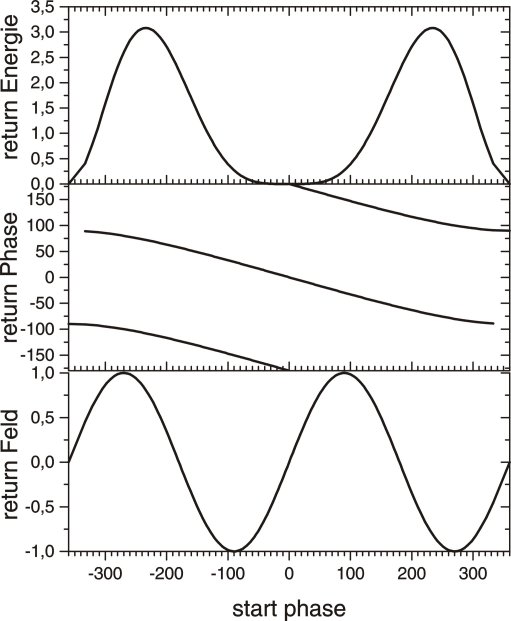
We interpret our finding as a direct consequence of electron-electron repulsion. The 1/r₁₂ potential forces the electrons into different regions in the three dimensional phase space. As a consequence for electrons to have equal parallel momentum requires some angle (i.e. transverse momentum) between them. The peak at p_ez1=p_ez2=1 a.u. is therefore most pronounced if at least one of the electrons has considerable transverse momentum. If in contrast one electron is fixed to move along the polarization axis the second electron is repelled longitudinal to be either faster or slower then the first one.

Figure 2
The horizontal axis gives the phase of the laser field at the instant of recollision
(a) return energy of the rescattered electron,
(b) initial phase at which the electrons was set free. The arrows i and ii indicate the threshold for excitation and ionization, respectivly
(c) electric field at return. The line indicate the critical field for over the barrier ionization of the first excited states (i) of Ar¹⁺
In most cases excitation occurs at return phases where the field is high enough quench the excited state instantaniously.

To discuss the measured distribution more quantitatively figure 3 shows the classically allowed region of phase space calculated within the rescattering model. We discuss the figure using the classical phase relations shown in figure 2.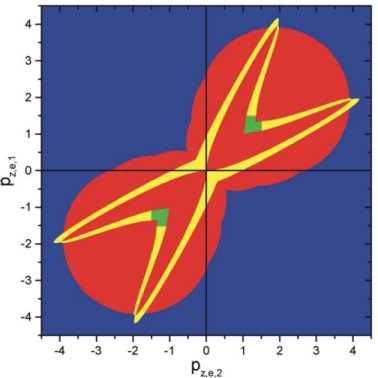

Figure 3
Classically allowed phase space within the rescattering model. The red area is for ionization the curved yellow line shows the locus of events for rescattering with excitation between the first excited state and the continuum, assuming instantanious quenching. The green area indicates the region of the most likely rescattering phase.

We point out that this curve in figure 2 relies on the fact that the excited electron will be field ionized instantaneously. If this is the case depends on the field at the return and thus also on the laser power and the atom under consideration. The critical field for over the barrier ionization can be estimated to be 2.97*10⁶ V/m for a binding energy of 11 eV (first excited state of Ar¹⁺).

Electron impact excitation shows dominant resonant structure. These resonances result from intermediate doubly excited states which autoionize. Once the returning electron has sufficient energy to ionize the two electrons can share their energy arbitrarily in the collision and then both acquire additional momentum from the field. The field determines a maximum return energy (3.17 times the pondoremotive potential) and hence a maximum momentum for the electrons. This region of phase space classically allowed for ionization is shown by the shaded area. Most of the intensity in our measured distributions is well within this classically allowed phase space.

From our data we conclude that at larger transverse momenta rescattering with excitation dominates while at smaller transverse momenta the (e,2e) ionization is dominant. In the latter channel electron-electron repulsion leads to the dominance of one fast electron accompanied by one slower.

Please check out M. Weckenbrock et al, J. Phys. B. 34 (2001) L449M. (120kb) for further information.