Electron capture in slow, highly charged ion collisions can be described by the classical over-barrier model [1].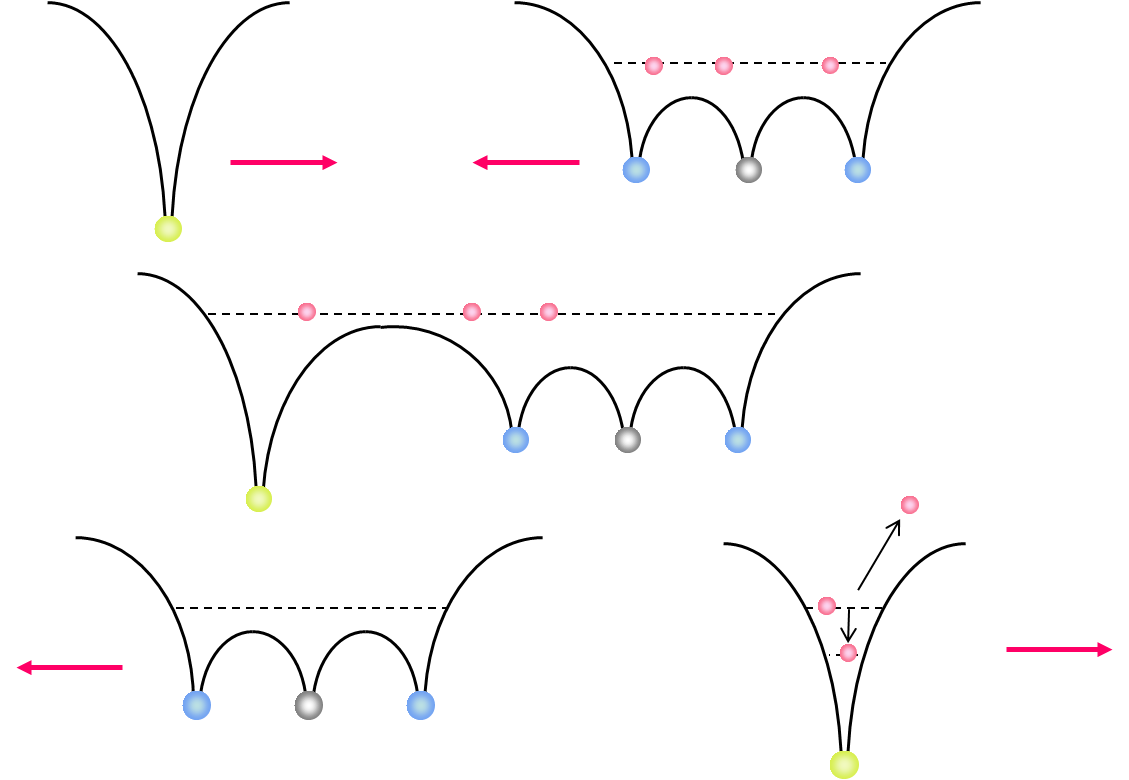

Figure 1: Classical Over-Barrier-Model

If a slow, highly charged projectile is moving into the target zone the Coulombic barrier between the projectile and the target decreases and the target electrons are ‘molecularized’. While the projectile is moving out of the reaction zone the Coulombic barrier between the projectile and the target rises up again. At this point there is a certain possibility that the molecular electrons can be captured either by the projectile or recaptured by the target core.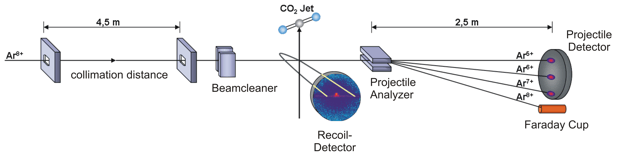

Figure 2: schematic diagram of the experimental setup; inside the spectrometer a cooled CO₂ gas jet is crossed by Ar⁸⁺ projectile ions. The different projectile charge states are separated by an analyzer and detected by a time- and position sensitive delay-line anode. The positively charged recoil ions are guided by a homogenous electrical field onto a second time- and position sensitive detector.

By making use of the COLTRIMS (COLd Target Recoil Ion Momentum Spectroscopy) technique we are able to observe the three-body dissociation of CO2³⁺ leading to C⁺ +O⁺ +O⁺ ions in a kinematically complete way. The detection of all fragments with 4p solid angle allows us to distinguish the various fragmentation mechanisms of the trication in unprecedented detail and completeness. The ion beam of Ar⁸⁺ projectiles at 3.2 keV/u has been generated at the Electron Cyclotron Resonance (ECR) Ion Source at Goethe-University, Frankfurt. The ionic fragments produced in the interaction region are guided by an electrical field of 39 V/cm onto a microchannel plate detector with delay-line anode. Downstream of the reaction zone the projectile charge states are separated by an electrostatic deflector. These projectile ions are detected by a time- and position sensitive microchannel plate detector, as well.

N. Neumann et al., Phys. Rev. Lett. 104, 103201, 2010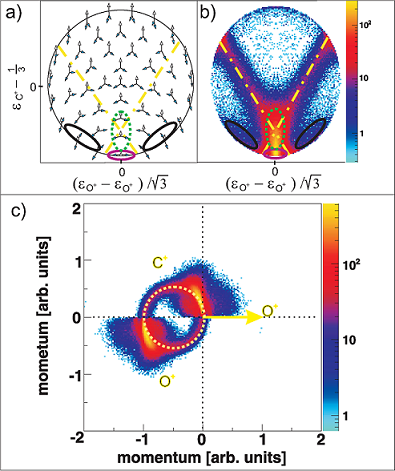

Figure 3: (a) Characteristic momentum vector geometries for specific points in the Dalitz plot and (b) Daltiz plot with measured data; Events located in the different marked areas correspond to various reaction mechanisms: magenta colored oval - direct ionization process, dash-dotted X-shape - sequential breakup, black ovals on left and right side - asynchronous stretching and green dotted area - molecular bending. (c) Newton diagram: momentum vector of one O⁺ ion in the CM frame defines the x-axis, while the relative momentum vectors of the C⁺ ion and the second O⁺ ion are mapped in the upper and lower half, respectively; the dashed circle marks the sequential breakup, the symmetric islands in the upper and lower half identify the direct and concerted breakup mechanism, see text.

A very useful tool for visualization of three body processes is the Dalitz plot [2]. This probability-density plot displays the vector correlation in terms of the reduced energies of the three atoms. A key advantage of the Dalitz plot is, that the phase space density is constant, i.e. all structure in such a plot results from the dynamics of the process, not from the trivial final state phase space density. Figure 3(b) shows a Dalitz plot of our measured data. Each region of that diagram refers to a certain geometry of the momentum vectors at the instance of breakup as shown in fig. 3(a). Our data clearly shows the various breakup mechanisms like the direct breakup (violet oval), the asynchronous dissociation mechanism preceded by molecular bending (green dotted ovel) and asymmetric stretching (black ovals) and the sequential reaction process (yellow dash-dotted lines).

To see the sequential breakup more directly, we display the same data in a Newton diagram in fig. 3(c). Here the momentum vectors are shown with respect to the center of mass (CM) of the fragments. The direction of the momentum vector of one of the O⁺ ions is represented by an arrow fixed at 1 a.u.. The momentum vectors of the C⁺ ion and the second O+ ion are normalized to the length of the first O⁺ ion momentum vector and mapped in the upper and lower half of the plot, respectively. In the Newton diagram the C⁺ and the second O⁺ fragment momenta are located on a circle shifted to the left by about half of the first O⁺ ion momentum. This shifted circle (marked by the dashed line in fig. 3(c)) is a clear proof of a two step dissociation mechanism. In the first step the CO2³⁺ molecule dissociates into an O⁺ ion and an CO2⁺ ion. Then after a delay, when the force of the departing O⁺ ion onto the CO2⁺ fragment is negligible, the second step occurs: the CO2⁺ ion, which is moving to the left, dissociates into a C⁺ ion and a second O⁺ ion.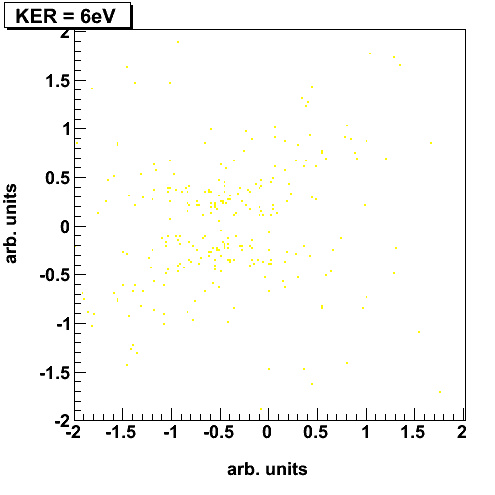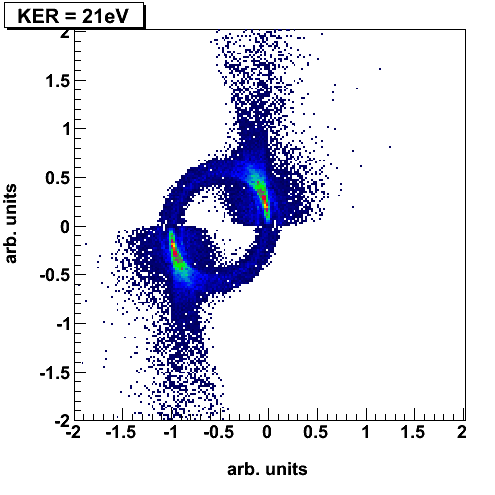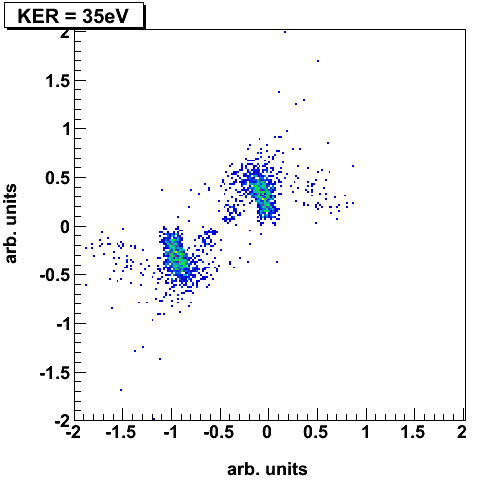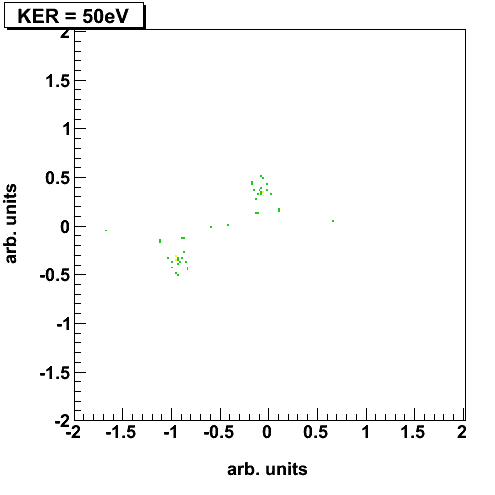

Figure 4: Newton diagram for different regions of KER.

The amount of energy deposited into the system by the ion impact is converted to kinetic energy of the fragments, which we measure. By varying the kinetic energy (KER) we can show that for different KER regions the various reaction mechanisms are active (see fig. 4). For KER regions barely above the threshold (KER < 17 eV) for the three body breakup the fragmentation proceeds predominantly in a two step, sequential fashion. If an additional Energy (17 eV < KER < 31 eV) is brought into the system some flux appears that corresponds to asymmetric stretching of the molecule before fragmentation. Also some population of the direct breakup channel occurs. For even higher KER (KER > 31 eV), finally, that direct breakup dominates.

Fragmentation Dynamics of CO23+ Investigated by Multiple Electron Capture in Collisions with Slow Highly Charged Ions
N. Neumann, D. Hant, L. Ph. H. Schmidt, J. Titze, T. Jahnke, A. Czasch, M. S. Schöffler, K. Kreidi, O. Jagutzki, H. Schmidt-Böcking and R. Dörner
Physical Review Letters, 104, 103201 (2010)
Paper on ArXiv.org
DOI: 10.1103/PhysRevLett.104.103201