Kinematically complete experimental study of Compton scattering at helium atoms near the ionization threshold

Compton scattering is one of the fundamental interaction processes of light with matter. When discovered, it was described as a billiard-type collision of a photon "kicking" a quasi-free electron. With decreasing photon energy, the maximum possible momentum transfer becomes so small that the corresponding energy falls below the binding energy of the electron. In this regime, ionization by Compton scattering becomes an intriguing quantum phenomenon. Here, we report on a kinematically complete experiment studying Compton scattering off helium atoms in that regime. We determine the momentum correlations of the electron, the recoiling ion and the scattered photon in a coincidence experiment based on cold target recoil ion momentum spectroscopy, finding that electrons are not only emitted in the direction of the momentum transfer, but that there is a second peak of ejection to the backward direction. This finding links Compton scattering to processes such as ionization by ultrashort optical pulses, electron impact ionization, ion impact ionization, and neutron scattering, where similar momentum patterns occur.

Two theoretical approaches have been used. Approach I uses a correlated two-electron wavefunction in the initial state with outgoing Coulomb waves with charge 1 as the final state. Approach II uses a single-active-electron model for the initial state, with a final scattering state in an effective potential.

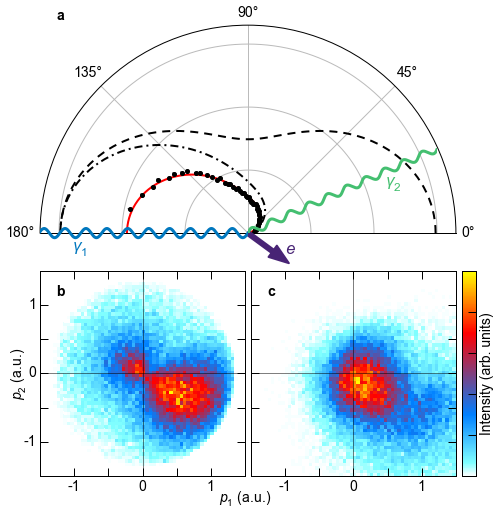
FIG. 1: Scheme of ionization by Compton scattering at hν=2.1 keV. a, The wavy lines indicate the incoming and outgoing photon, and the purple arrow depicts the momentum vector of the emitted electron. The dashed line shows the Thomson cross-section, that is, the angular distribution of a photon scattering at a free electron. Black dots show the experimental photon angular distribution for ionization of He by Compton scattering, integrated over all electron emission angles and energies below 25 eV. The photon momenta are determined using the electron and ion momenta, as well as momentum conservation. The statistical error is smaller than the dot size. The dash-dotted line shows the A² approximation for all electron energies and the solid red line shows the A² approximation for electron energies below 25 eV. The calculations were done using Approach I. The solid and dash-dotted lines are multiplied by a factor of 1.9. b, Momentum distribution of electrons emitted by Compton scattering of 2.1 keV photons at He. The coordinate frame is the same as in a: the scattering plane is defined by the incoming (horizontal) and scattered photon (upper half plane); that is, p₁ is the electron momentum component in the k₁ direction and p₂ is the component perpendicular to k₁ within the scattering plane. The momentum transfer points to the forward lower half plane. The data are integrated over the out-of-plane electron momentum components. c, He⁺ ion momentum distribution for the same conditions as in b.

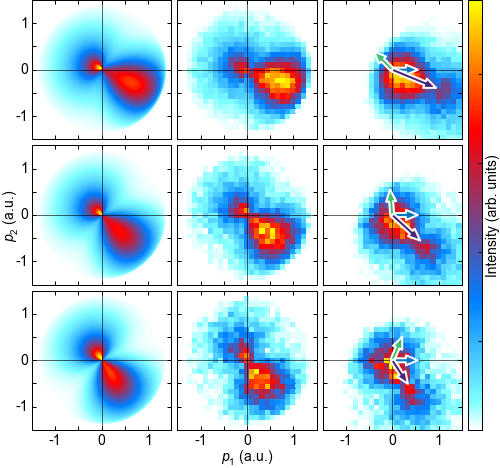
FIG. 2: Electron and ion momentum distributions for different momentum transfer gates. In all panels, p₁ is the momentum component in k₁ direction, p₂ is the component perpendicular to k₁ within the scattering plane. a-c, Electron momentum distributions obtained from modeling within the A₂ approximation using Approach II. d-f, Electron momentum distributions measured by our experiment. g-i, Measured momentum distributions of the ions. From top to bottom, the rows correspond to different momentum transfers Q = 1.0, 0.8, and 0.6 a.u., respectively. The arrows in the third column indicate the photon momentum configuration for each row. Here, the blue arrows represent the momentum of the incoming photon, the light green arrows the momentum of the scattered photon, and the dark purple arrows the momentum transfer.

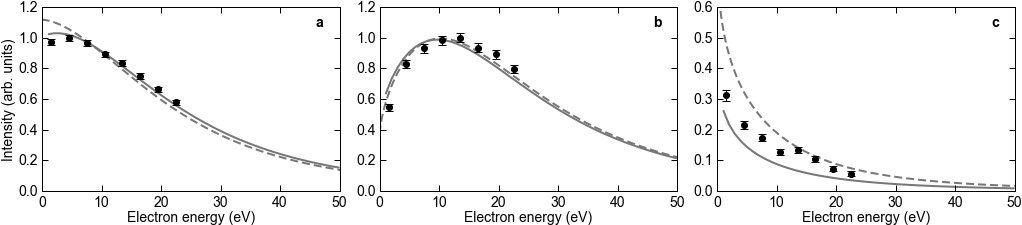
FIG. 3: Electron energy distribution. The scattering angle between the incoming and outgoing photon for the outgoing photon is restricted to 140 < θ < 180° in all panels. a, The electron energy spectrum is shown independent of the electron emission direction. b, The electron emission angle is restricted to forward scattering (0 < θ_e < 40°). c, The electron emission angle is restricted to backward scattering (140 < θ_e < 180°). The black dots are the experimental data. The error bars represent the standard statistical error. The solid lines are the theoretical results of Approach I and the dashed lines are the results of Approach II. The experimental data in a and b are normalized such that the maximum intensity is 1; the theory is normalized such that the integrals of the experimental data and the theoretical curves are equal. The normalization factors in c are identical to those in b, because here we depict the forward/backward direction of the same distribution.

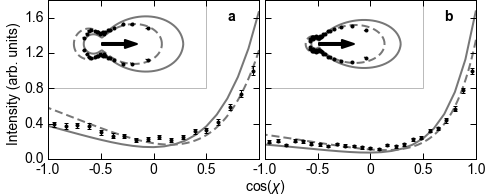
FIG. 4: Fully differential electron angular distributions. a, b, The photon scattering angle is 130 < θ < 170°. Displayed is the cosine of the angle χ between the outgoing electron and the momentum transfer Q for electron energies of 1.0 < E_e < 3.5 eV (a) and 3.5 E_e < 8.5 eV (b). Insets show the same data in polar representation, where the arrow indicates the direction of momentum transfer. Black dots are the experimental data, normalized such that the maximum is 1. Error bars represent the standard statistical error. The solid and dashed lines are the theoretical curves resulting from Approach I and Approach II, respectively. The theoretical curves are normalized such that the integral of experiment and theory are equal.

Publication:
Kinematically complete experimental study of Compton scattering at helium atoms near the ionization threshold
Max Kircher, Florian Trinter, Sven Grundmann, Isabel Vela-Perez, Simon Brennecke, Nicolas Eicke, Jonas Rist, Sebastian Eckart, Salim Houamer, Ochbadrakh Chuluunbaatar, Yuri V. Popov, Igor P. Volobuev, Kai Bagschik, M. Novella Piancastelli, Manfred Lein, Till Jahnke, Markus S. Schöffler, and Reinhard Dörner
DOI: 10.1038/s41567-020-0880-2
Nat. Phys. (2020)
 
See online:
Nature
Article PDF
arXiv
Pressemitteilung der Universtität