Magnetic fields alter strong-field ionization

When a strong laser pulse induces the ionization of an atom, momentum conservation dictates that the absorbed photons transfer their momentum p_γ=E_γ/c to the electron and its parent ion. Even after 30 years of studying strong-field ionization, the sharing of the photon momentum between the two particles and its underlying mechanism are still under debate in theory. Corresponding experiments are very challenging due to the extremely small photon momentum (10^-4 a.u.) and their precision has been too limited, so far, to ultimately resolve the debate.

Here, by utilizing a novel experimental approach of two counter-propagating laser pulses, we present a detailed study on the effects of the photon momentum in strong-field ionization. The high precision and self-referencing of the method allows to unambiguously demonstrate the action of the light's magnetic field on the electron while it is under the tunnel barrier, confirming theoretical predictions, disproving others. Our results deepen the understanding of, for example, molecular imaging and time-resolved photoelectron holography. The theoretical simulations were done by Simon Brennecke and Manfred Lein from the university of Hannover, Germany.

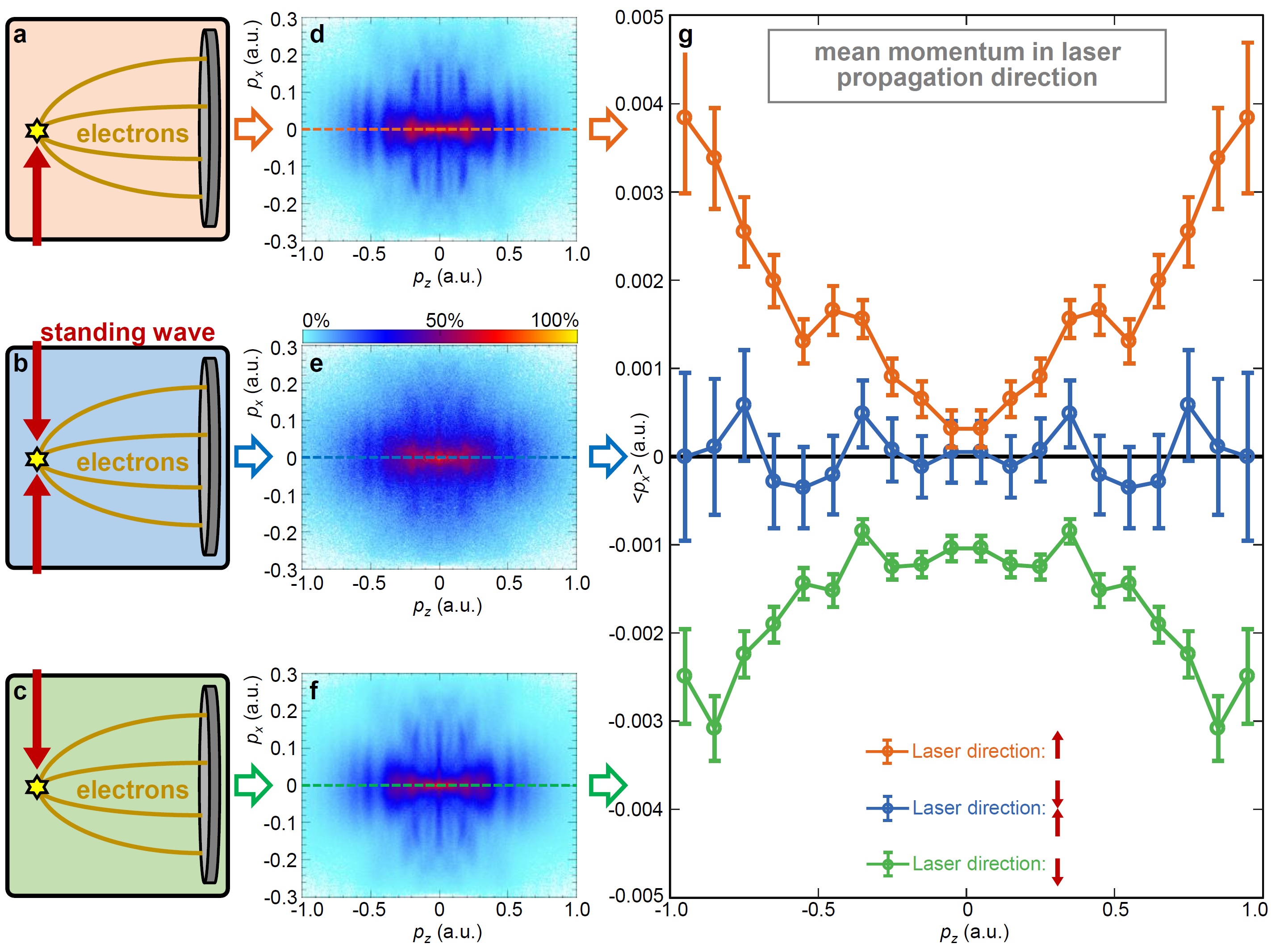
Figure 1: Experimental scheme. a-c, The experimental setup allows for three different geometries for strong-field ionization of argon. The laser can enter the interaction chamber either from one side individually (a, c) or from both sides simultaneously, creating a standing wave (b). d-f, The corresponding electron momentum distributions obtained for linear light do not seem to exhibit any offsets caused by the photon momentum, i.e. not showing any asymmetrical features along light propagation axis. g, By calculating the mean momentum in light propagation direction for all three ionization scenarios and zooming in by a factor of ~100, clear non-dipole features become visible. In the case of ionization by a standing wave, no significant momentum offset arises, because of the spatial symmetry of the experimental arrangement. In the two cases of ionization by a single laser pulse from just one side, the parabolic shape flips sign when flipping the propagation direction of the laser pulse. The error bars show statistical errors.

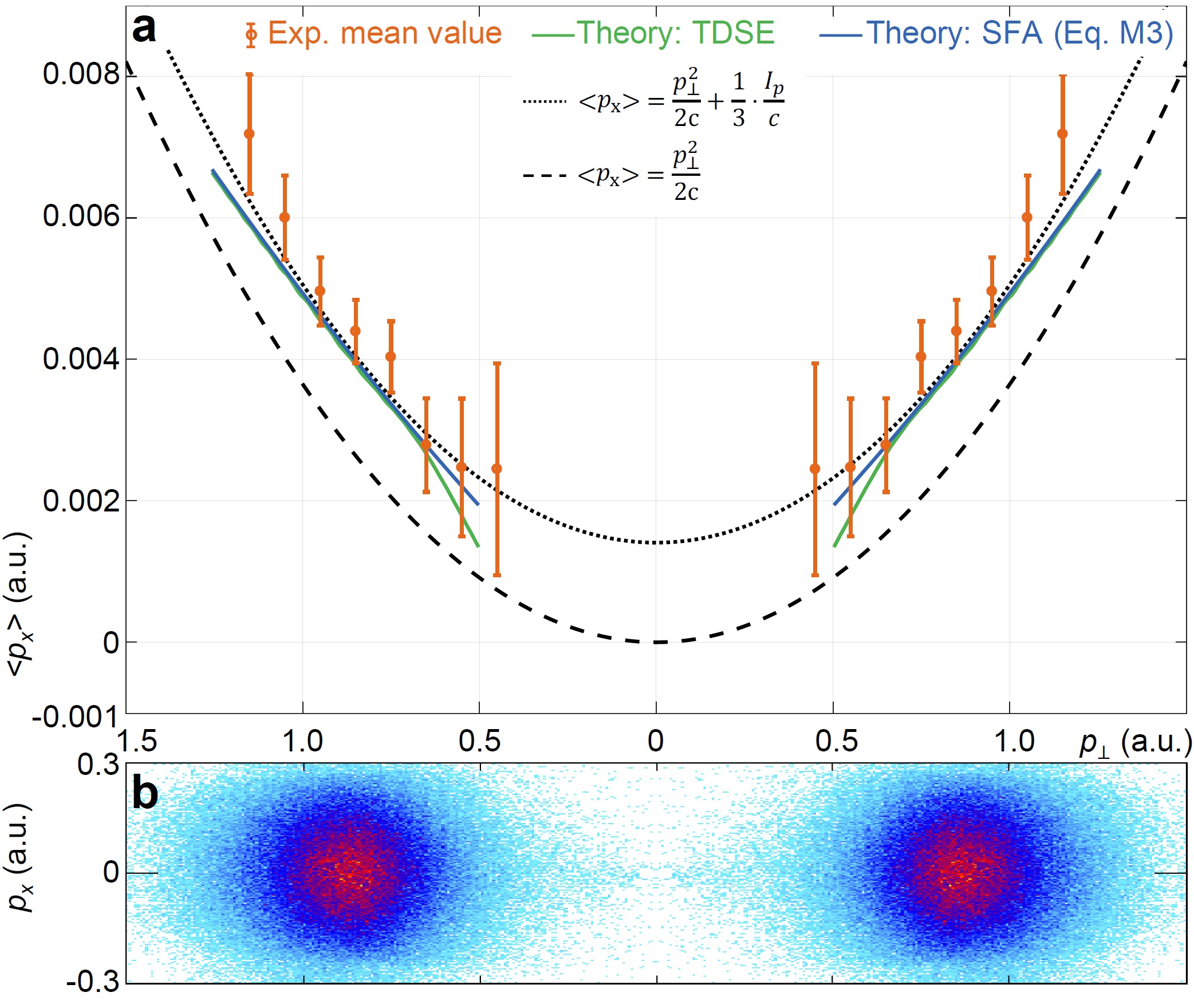
Figure 2: Results for circularly polarized light. a, The mean electron momentum in light propagation direction p_x is plotted against the radial momentum |𝑝_⊥| obtained by using circularly polarized light at 1.7×10¹⁴ W/cm²; note the scale of ~ 10^-3 a.u. Error bars show statistical errors. The description of the theoretical results can be found in the original publication. b For visual orientation the experimental two-dimensional momentum distribution is displayed within the same coordinate frame as in a.

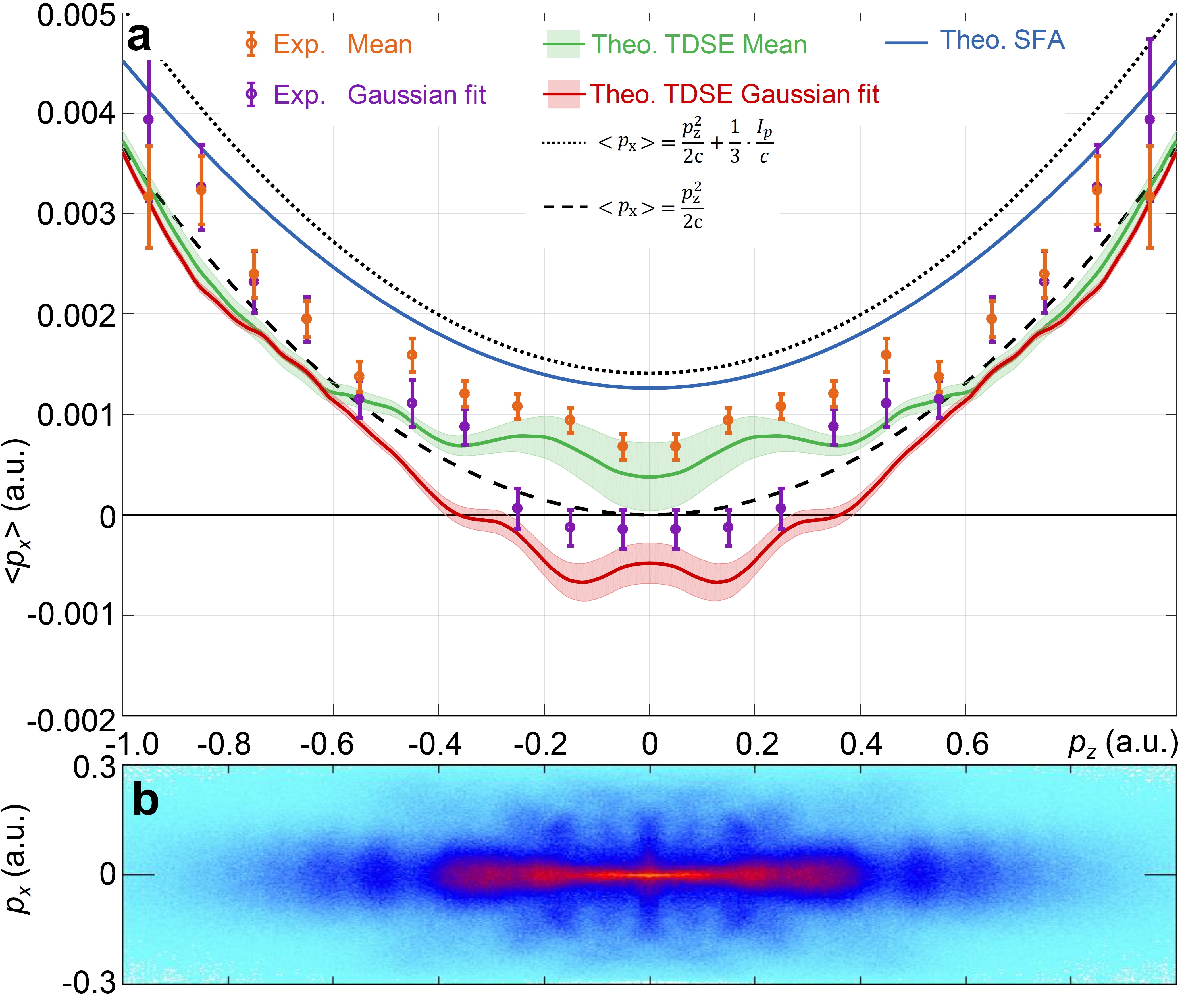
Figure 3: Results for linearly polarized light. a, The mean electron momentum in light propagation direction p_x is plotted against the momentum in direction of the light’s polarization axis p_z obtained by using linearly polarized light at 1.1×10¹⁴ W/cm²; note the scale of ~ 10^-3 a.u. Experimental error bars show statistical errors. The description of the theoretical results can be found in the original publication. b For visual orientation the experimental two-dimensional momentum distribution is displayed within the same coordinate frame as in a.

Figure 4: Experimental setup., The technical drawing of the newly constructed COLTRIMS reaction microscope shows an intersection of the experimental construction. Individual gas atoms, which fly down through the vertical tube in the picture, are ionized by a highly intensive laser. The beam path of the laser is illustrated on the table in the back. The momenta of the electrons and ions that are produced in the reaction are measured with high precision by the horizontally depicted bronze-coloured spectrometer in the vacuum chamber.

Publication:
Magnetic fields alter strong-field ionization
Alexander Hartung, Sebastian Eckart, Simon Brennecke, Jonas Rist, Daniel Trabert, Kilian Fehre, Martin Richter, Hendrik Sann, Sefan Zeller, Kevin Henrichs, Gregor Kastirke, Josef Hoehl, Anton Kalinin, Markus Schöffler, Till Jahnke, Lothar Ph. H. Schmidt, Manfred Lein, Maksim Kunitski and Reinhard Dörner
DOI: 10.1038/s41567-019-0653-y
Nat. Phys. (2019)
 
See online:
Nature Physics
arXiv