Atomic physics at storage rings

Within the present research topic we explore the opportunities offered by microscopic liquid jets for applications at storage rings, both in terms of advanced research infrastructure and as a novel route for the investigation of so far unexplored light-matter interaction phenomena. One of the scientific caterpillars at the future Facility for Antiproton and Ion research (FAIR) facility at GSI is represented by the highly complex internal-target experiments at the High-Energy Storage Ring (HESR). Here, atomic and nuclear physics experiments foreseen within the SPARC and PANDA collaborations, respectively, with the latter representing a state-of-the-art universal detector for antiproton-proton reaction measurements, aim at addressing fundamental issues of QED and QCD, including atomic structure investigations and key aspects of quark confinement and gluon dynamics. In this regard, the use of the internal targets provides the highest efficiency in terms of the luminosity, a particularly crucial aspect for the investigation of processes that are characterized by extremely small cross sections.

State-of-the-art internal targets for storage-ring experiments are realized by producing a cluster beam, i.e., by expanding a gas through a nozzle into vacuum, yet the typically low-density of cluster gas jets generally precludes their use for the planned experiments at FAIR. On the other side, the vacuum expansion of a supercritical fluid or even a liquid is fundamentally different in nature when compared with a gas jet expansion. In particular, the dramatic narrowing of the liquid beam angular spread occurring upon cooling of the source down into the two-phase supercritical regime, and eventually well into the liquid phase (click here to read more), would allow, in turn, adjusting the spatial density over several orders of magnitude at some given distance down stream from the nozzle due to mass conservation. We have demonstrated this recently at the Experimental Storage Ring (ESR) at GSI (Kühnel et al., 2009), by improving the highest area density by orders of magnitude over previous results achieved at the ESR by employing a cluster jet target.

Whereas these results clearly provide a major step towards the goal of achieving higher target densities for experiments at storage rings, only very little is known about the details of interaction of a relativistic highly charged ion (HCI) with a dense liquid droplet, especially because energy losses scale with the square of the charge number. In order to address this fundamental issue, we have recently measured the energy loss of relativistic HCIs during the interaction with a hydrogen droplet target beam (Petridis et al., 2011). Figure 1 shows our experimental results (data points) compared with theoretical predictions (dashed lines) obtained by assuming a hydrogen target density that is several orders of magnitude smaller than the local droplet liquid density. The fact that the experimental energy losses are orders of magnitude smaller than expected might at first sight appear surprising. To understand this, we have roughly estimated the number of HCIs that are involved in direct collisions (per turn) with the droplets and we have found that this corresponds to a tiny fraction of only 0.01 % of the total number of stored ions. Upon collision with a HCI the droplet likely disintegrates, producing both neutral and ionized atoms and larger fragments. Since this fragmentation process typically occurs on the picosecond (10^-12 s) time scale, we have argued that the experimentally measured energy losses are primarily dominated by the in-teraction of the HCIs that are not involved in direct collisions with the nearly spatially uniform target consisting of the fragmentation products (Petridis et al., 2011).

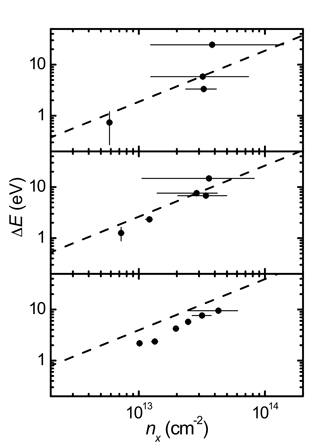Figure 1. Experimental (filled symbols) ion energy losses per turn of U⁹¹⁺ at 400 MeV/u (top panel), U⁹¹⁺ at 216 MeV/u (middle), and U⁸⁹⁺ at 116 MeV/u (lower panel), measured as a function of the mean hydrogen target area density. The dashed lines are theoretical results based on the Bethe-Bloch formula. (From Petridis et al., 2011).

These initial experiments, which hint at a very complex physical picture concerning the interaction of HCIs with microscopic liquid droplets, not only are expected to have a profound impact on the development of future internal target experiments at storage rings, but they also open up new exciting possibilities for the investigation of the interaction of HCIs and matter. From the physical point of view, only very little is known about the details of the heating mechanism(s) leading to the droplet disintegration process induced by a single HCI, yet this kind of interaction is particularly appealing as in many respects it may resemble that occurring in intense ultra-short laser-matter interactions. In particular, at the HESR it will be possible to store HCIs at energies corresponding to a Lorentz factor γ ≈ 6 (see Fig. 2), i.e., to the ultra relativistic regime. Due to the Lorentz contraction the transverse electric field produced by these relativistic ions acts like an ultra-short light pulse that can be spectrally decomposed into virtual photons with energy of up to 1 MeV. The use of liquid droplet beams at the HESR has thus the great potential to open the route to the investigation of so far unexplored interaction phenomena.

: Figure 2. Angular dependence of the radial electric field strength produced by a single ion moving with a relative velocity β = v/c, with c the light speed. Adapted from J. Eichler, Phys. Lett. A 347, 67 (2005).