Ultrafast Preparation and Detection of Ring Currents in Single Atoms
Within the Bohr model, the electron travels around the nucleus on circular orbits possessing quantized orbital angular momentum associated with a ring current. In quantum mechanics this motion is reflected by the magnetic quantum number m.
If a strong electric field is applied to an atom, an electron can be liberated by tunnel ionization. We investigate the influence of the magnetic quantum number m on the tunneling process in the regime of non-adiabatic tunneling (i.e. temporal evolution of the driving electric field cannot be neglected). Performing a pump-probe experiment, the transmission probability through a rotating tunnel is analyzed and it is shown that the ionization probability as well as the final momentum distribution depend on the sign of the magnetic quantum number m. We conclude that electrons that are counter rotating with respect to the laser’s electric field are preferred for ionization and that angular momentum is partially conserved during tunneling.
The gained insights can be used to prepare and detect ring currents in single atoms on ultrafast timescales. Fig. 1 shows how the preparation is done starting with argon in its ground state. Depending on the helicity of the ionizing laser pulse the ring current with defined sign is prepared in a singly charged argon atom.
Having prepared the argon atom in one of the two possible states (that are degenerate in energy and only differ in the sign of their quantum phase) a probe pulse is applied long after the pump pulse is gone (200 fs later) detecting the sign of the ring current. Independent of the pump step the same probe pulse is used in all cases (electric field of the probe pulse rotates clockwise).
Fig. 2 shows the electron momentum distribution of the second electron for two scenarios. The upper row shows the case where pump and probe rotate in the same direction. The lower row shows the case in which pump and probe have the same helicity. While at first glance both distributions appear to be similar, detailed examination unveils slight differences, which become prominent in the corresponding angle-integrated kinetic energy spectra of the 2nd electron. From these energy spectra the energy dependent yield for the double ionization of argon can be obtained for m = -1 and m = +1. This result is shown in Fig. 3.

Figure 1 | Experimental preparation of ring currents by m-dependent tunnel-ionization. a, The circular polarized laser pulse with a counter-clockwise rotating electric field liberates an electron by tunnel-ionization at t = 0 fs. Clockwise rotating electrons (m = + 1) are strongly preferred for ionization. b, Step a results in a persistent ring current in the remaining ion. d and e, The corresponding process for an electric field with inverted helicity. The sign of m and the direction of the ring current are inverted as well.
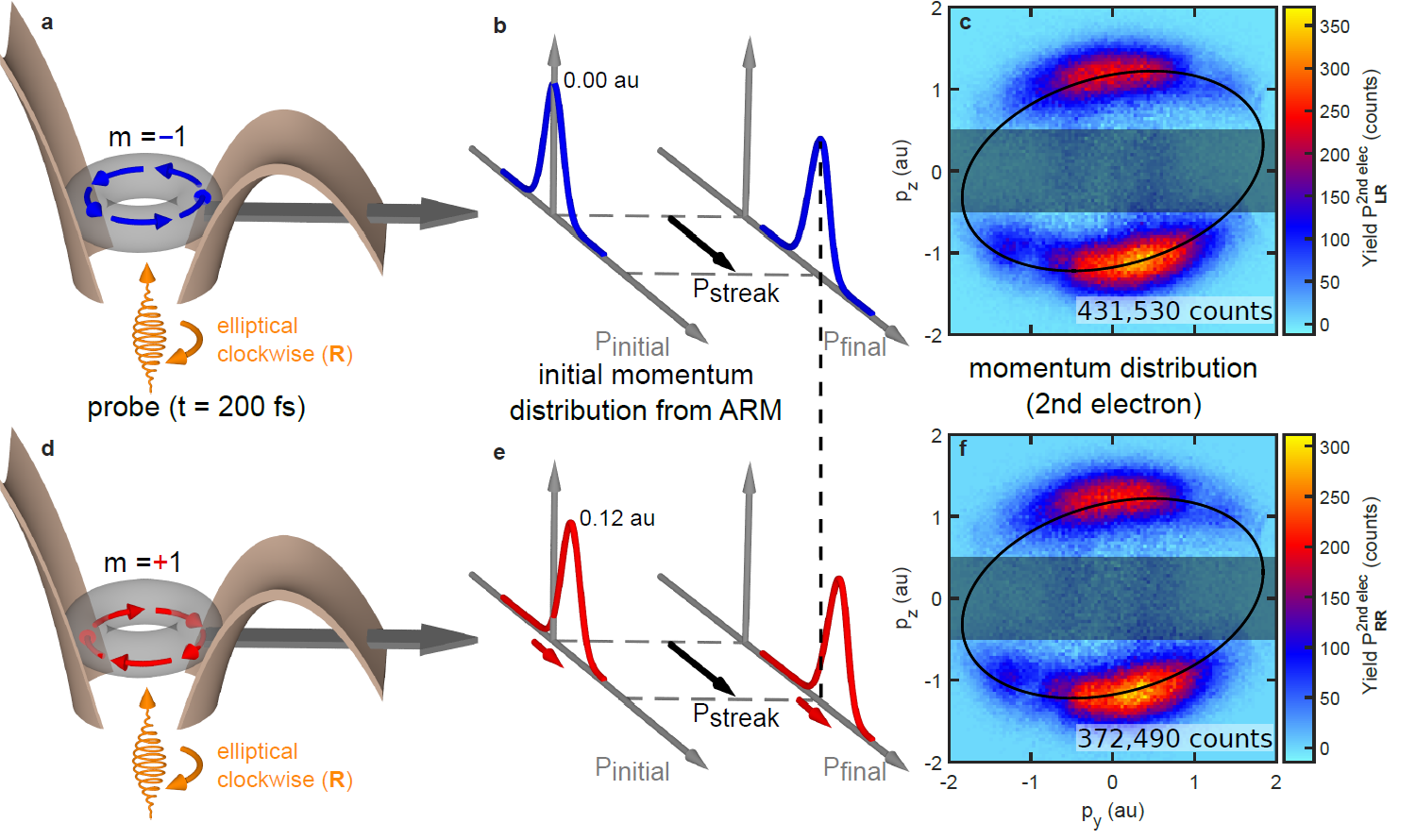
Figure 2 | Detection of ring currents by momentum resolved m-dependent tunnel-ionization. a and d , At t=200 fs the elliptically polarized probe pulse with clockwise rotating electric field hits the ion that has been created by the pump pulse (see Fig. 1). c and f, The second electron’s momentum distributions PLR and PLR for equal acquisition times (the first electron, measured in coincidence, is selected to fulfill |pz_calc| <0.5 a.u.). There are more events in PLR than in PRR, proving that the sign of the magnetic quantum number influences tunnel ionization. The electron’s “initial” momentum distributions after tunneling from ARM theory (dashed lines in panels b, e), with m= +1 has higher momentum (peak at p = 0.12 a.u.) than m = -1 (peak at p = 0.12 a.u.). These add to the drift momentum imparted by the laser pulse leading to different final radial momenta (solid lines in b, e).
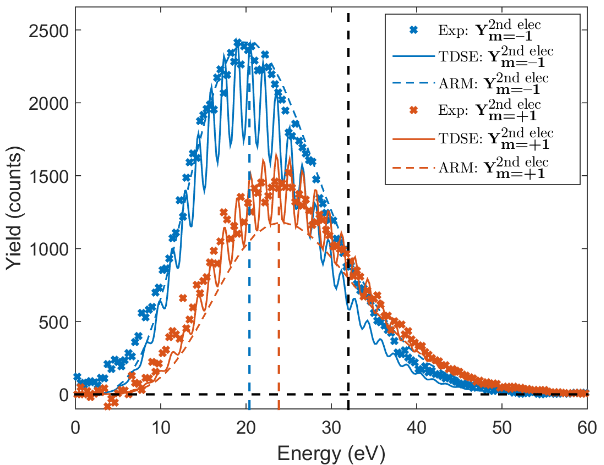
Figure 3 | Energy resolved electron spectra showing ring current transport during tunneling. Experimental energy dependent yields for the second electron are obtained for m= -1 and for m= +1. The experimental result is compared with our theoretical results (ARM theory) and numerical simulations of the time-dependent Schrödinger equation.
Publication:
Ultrafast Preparation and Detection of Ring Currents in Single Atoms
Sebastian Eckart, Maksim Kunitski, Martin Richter, Alexander Hartung, Jonas Rist, Florian Trinter, Kilian Fehre, Nikolai Schlott, Kevin Henrichs, Lothar Ph. H. Schmidt, Till Jahnke, Markus Schöffler, Kunlong Liu, Ingo Barth, Jivesh Kaushal, Felipe Morales, Misha Ivanov, Olga Smirnova, and Reinhard Dörner
DOI: 10.1038/s41567-018-0080-5
Nat. Phys. (2018)
Ringströme in einzelnen Atomen
S. Eckart, M. Kunitski, R. Dörner
DOI: 10.1002/piuz.201870404
Physik in unserer Zeit, 49 (2018) 162-163
See online:
Nature Physics
arXiv
